Sigma Squared model
This is a simplified and user-friendly model that allows to directly import spot size measurements into a FRED simulation. As the name is describing, the model is based on fitting the beam spot size using a second order polynomial, as described in the emittance model section:
Let’s take as a reference the case described by the following plot, showing the spot size measurements (blue stars) in the x direction taken at 5 different positions around the isocenter for a 100 MeV beam in a cyclotron facility.
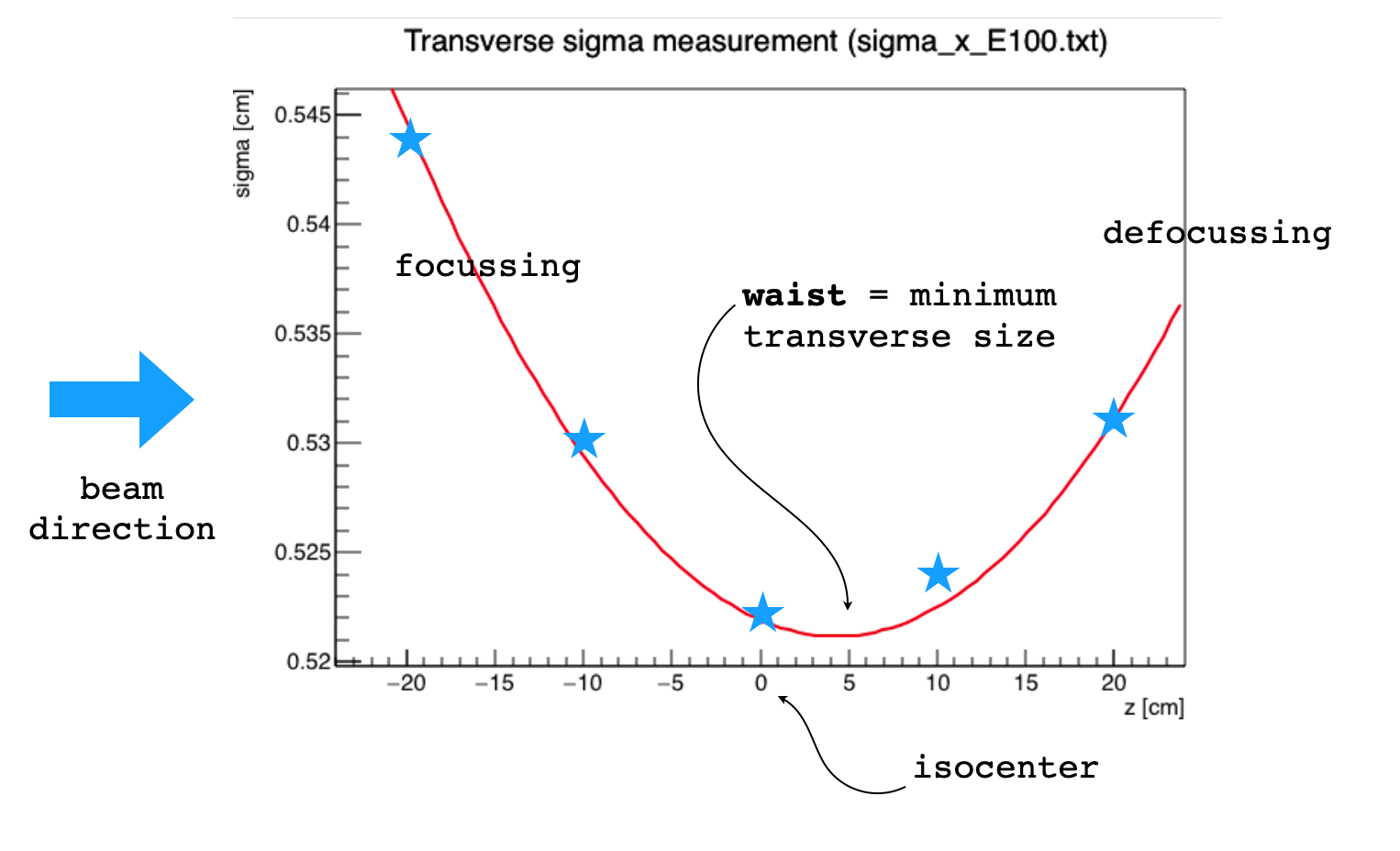
By fitting a parabolic function through the squares of the measured points
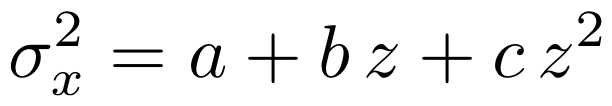
we can obtain the parameters needed for the emittance model
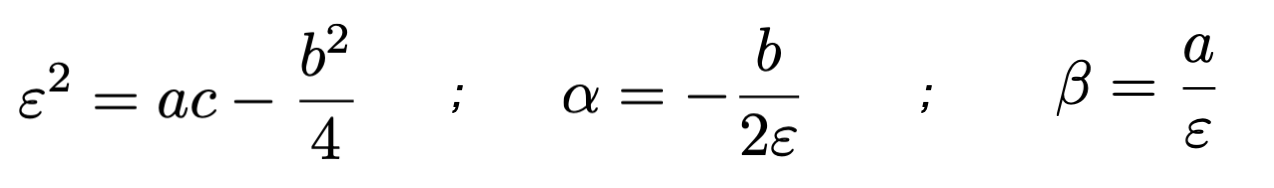
Example of a simple calculation in python using the measurements of previous Figure
from math import *
import numpy as np
import matplotlib
matplotlib.use('TkAgg')
import pylab as plt
zmeas = np.array([-20,-10,0,10,20])
sigmeas = np.array([0.544,0.530,0.522,0.524,0.531])
[[c,b,a],cov] = np.polyfit(zmeas,sigmeas*sigmeas,2,cov=True)
print('a=',a)
print('b=',b)
print('c=',c)
zmodel = np.linspace(np.min(zmeas),np.max(zmeas),400)
sigmasqr = a+b*zmodel+c*zmodel*zmodel
plt.ion()
plt.plot(zmodel,np.sqrt(sigmasqr),'-r',label='sigma squared model')
plt.plot(zmeas,sigmeas,'*b',label='data',markersize=10)
plt.legend()
plt.ylim(0,0.8)
plt.grid()
plt.xlabel('beam axis coordinate (cm)')
plt.ylabel('spot size (cm)')
plt.show()
input('return')
which gives in output
a= 0.27326425714285724
b= -0.0003427399999999939
c= 3.9535714285714174e-05
Important
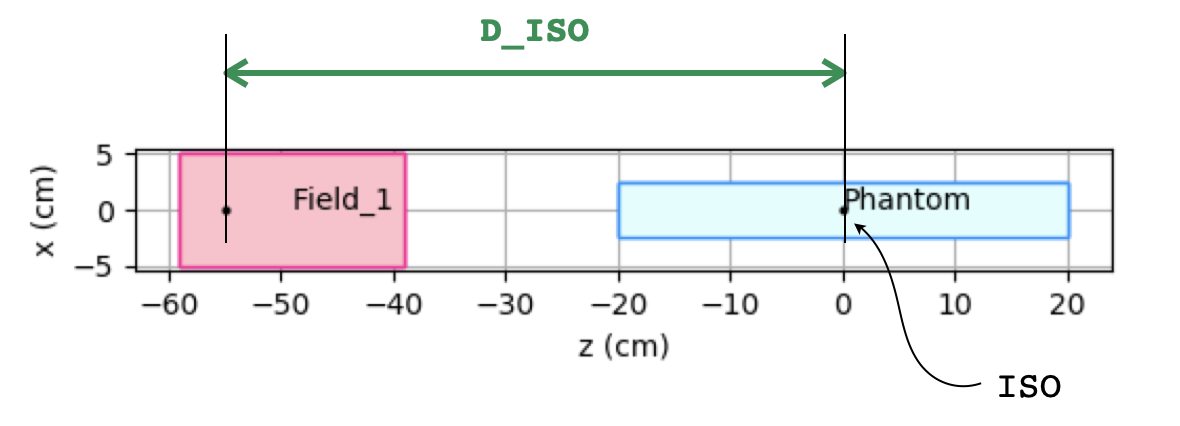
In the previous example, the parameters have been obtained with respect to the isocenter position which is at coordinate z=0 cm along the propagation direction. Since particles are generated in the field FoR, we have to inform FRED of the distance from field origin to the isocenter in order to have the correct spot size evolution along the beam axis. To this purpose, we define D_ISO has the distance of pencil beam origin and the isocenter.
- sigmaSqrModel = [D_ISO, aX, bX, cX, aY, bY, cY]
D_ISO : distance (cm) from pencil beam origin to ISO center plane
aX, bX, cX : interpolation parameters for sigma_x as described above
aY, bY, cY : interpolation parameters for sigma_y as described above
parmeters for Y are optional: if not present, the values of X are mirrored
The input lines for source definition using the sigma squared model model syntax are
field: 1 ; O = [0,0,-55]; L=[10,10,20]; pivot = [0.5,0.5,0.2]
pb: 1 1 ; particle = proton; T = 100; sigmaSqrModel = [55,0.27326425714285724,-0.0003427399999999939,3.9535714285714174e-05]
The evolution of beam cross section using the sigma squared model is represented by the following Figure
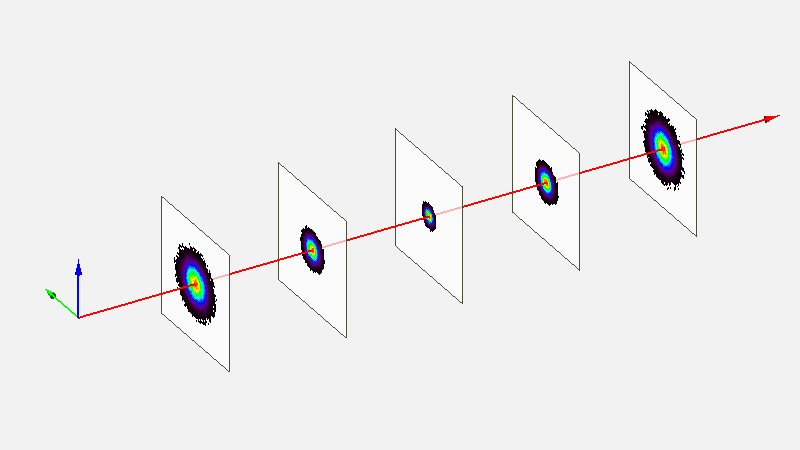
Note
The sigma squared model overrides any previous declaration concerning the beam envelope such as Xsec or FWHM. So these parameters are not needed and can be undefined.
Examples
Single-line input
Three spots using pb: directive in single-line mode:
region: phantom; L=[10,10,0.1]; voxels=[101,101,1]; pivot=[0.5,0.5,0]; material=PMMA
field: 1 ; O = [0,0,-200] ; L = [20,20,2] ; pivot = [0.5,0.5,0.5]
pb: 1 1; particle=p; E=70; N=1e7; v=[-2,0,200]; sigmaSqrModel=[200,0.36343,0.00294,0.00004731]
pb: 2 1; particle=p; E=80; N=2e7; v=[ 0,0,200]; sigmaSqrModel=[200,0.47652,0.00285,0.00004755]
pb: 3 1; particle=p; E=90; N=3e7; v=[+2,0,200]; sigmaSqrModel=[200,0.49745,0.00300,0.00004342]
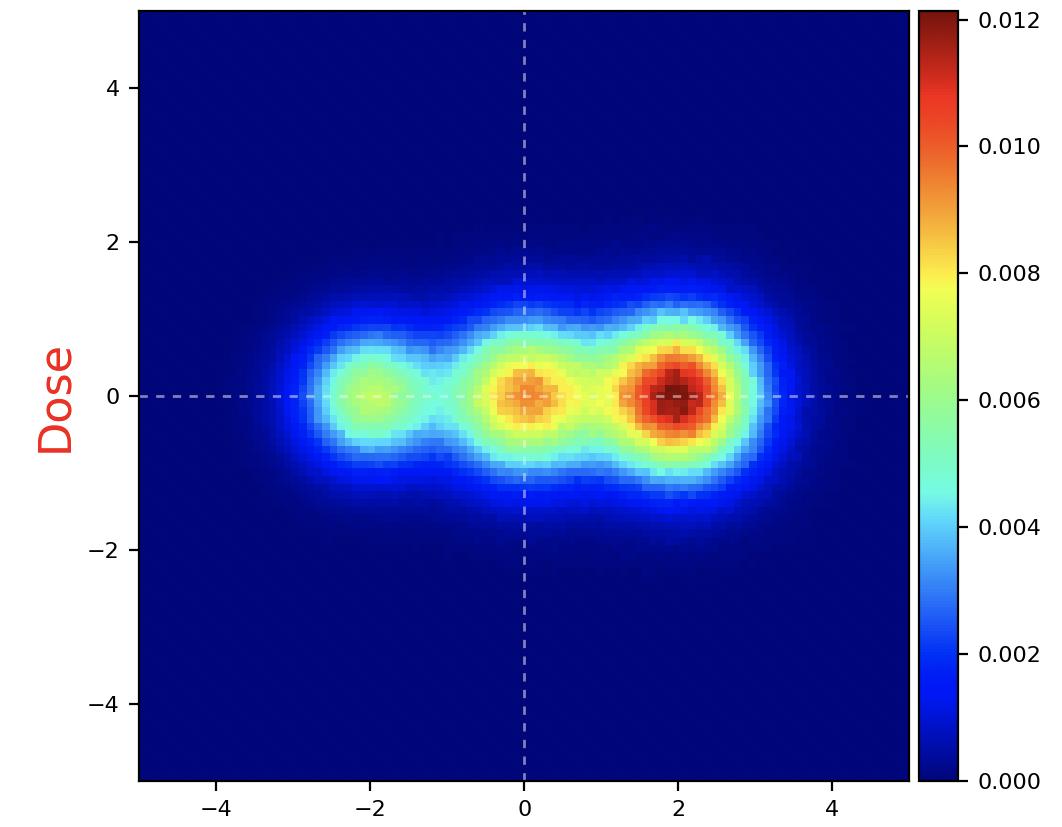
Column-mode input using pbmaster
Three spots using pbmaster: directive to define common parameters, e.g. field to ISO distance. Equivalent to previous example, but more compact. Useful when dealing with thousands of PBs, for instance in a patient treatment plan.
region: phantom; L=[10,10,0.1]; voxels=[101,101,1]; pivot=[0.5,0.5,0]; material=PMMA
field: 1 ; O = [0,0,-200] ; L = [20,20,2] ; pivot = [0.5,0.5,0.5]
pbmaster: 1 ; particle=p; sigmaSqr_D_ISO=200; v.z=200; columns=[E,N,v.x,v.y,sigmaSqr_aX,sigmaSqr_bX,sigmaSqr_cX]
pb: 1 1 70 1e7 -2 0 0.36343 0.00294 0.00004731
pb: 2 1 80 2e7 0 0 0.47652 0.00285 0.00004755
pb: 3 1 90 3e7 +2 0 0.49745 0.00300 0.00004342
The parameters that you can predeclare in the pbmaster: directive have to following names: sigmaSqr_D_ISO,sigmaSqr_aX,sigmaSqr_bX,sigmaSqr_cX,sigmaSqr_aY,sigmaSqr_bY,sigmaSqr_cY.