Emittance model
In the emittance model the evolution of the spot size can be described using the Twiss parameters
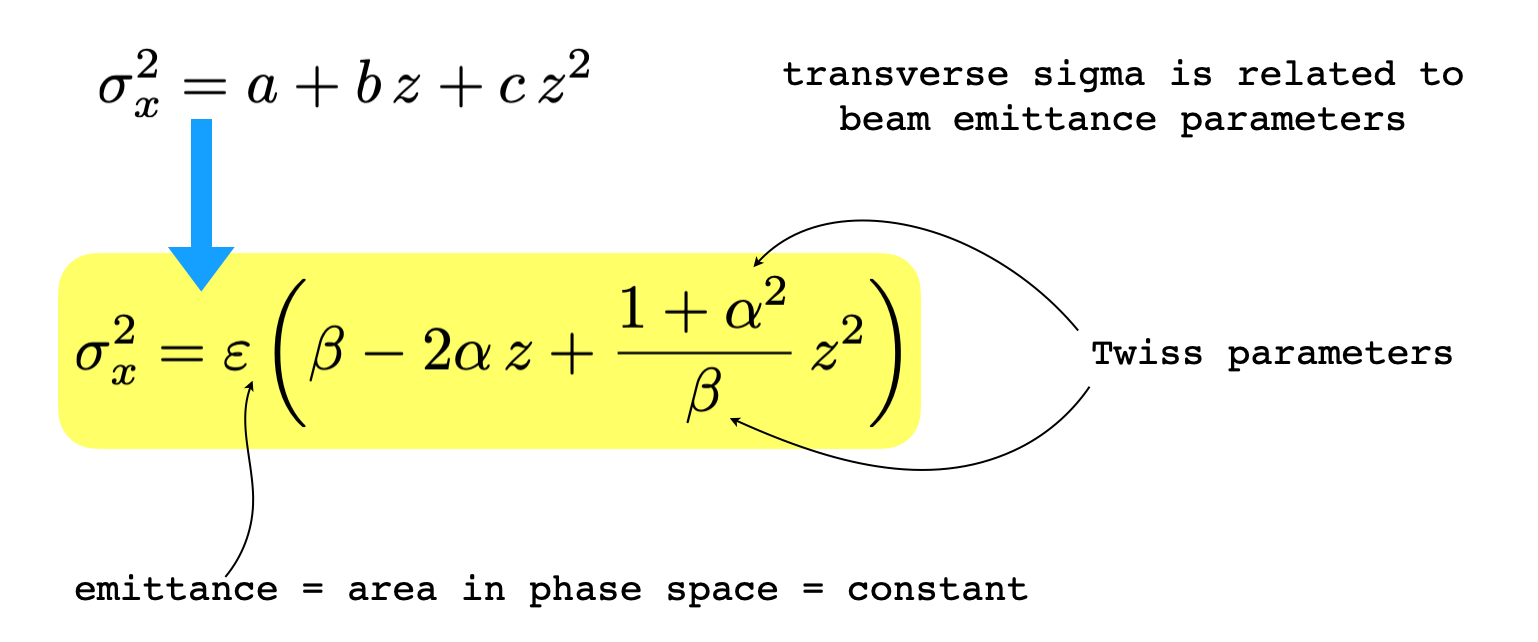
where the square of the std deviation \(\sigma_x^2\) along \(x\) is a quadratic function of propagation coordinate \(z\).
The model parameters are the emittance \(\varepsilon\), and the Twiss parameters \(\alpha\) and \(\beta\).
To use the emittance model, the following parameters must be set in a pencil beam definition:
- Xsec = emittance
activate the emittance model: the cross-section is automatically a bivariate gaussian distribution
- emittanceX = (float)
emittance along x
- twissAlphaX = (float)
Twiss alpha along x
- twissBetaX = (float)
Twiss beta along x
- emittanceY = (float) [emittanceX]
emittance along y
- twissAlphaY = (float) [twissAlphaX]
Twiss alpha along y
- twissBetaY = (float) [twissBetaX]
Twiss beta along y
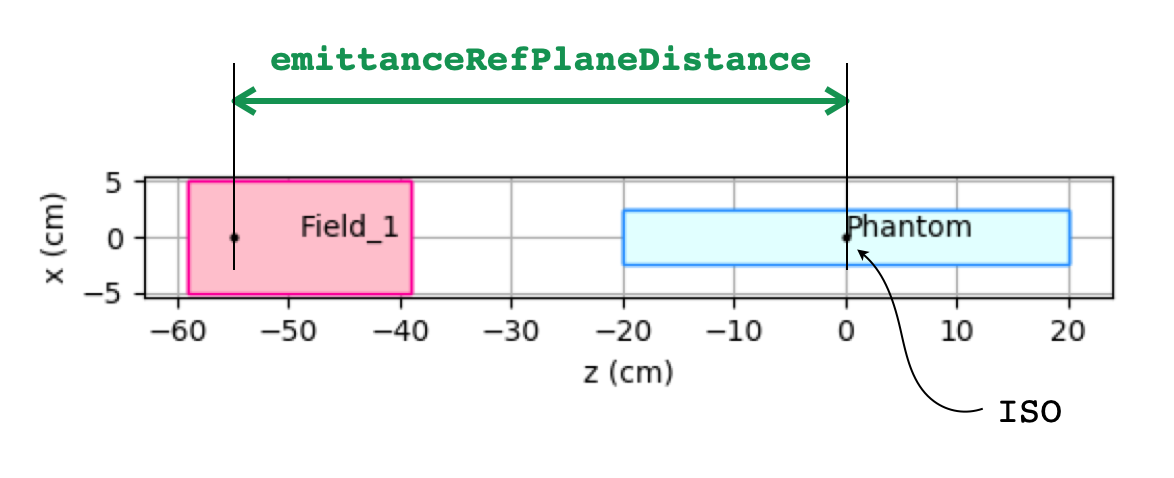
- emittanceRefPlaneDistance = (float)
distance from beam origin of the reference plane where the previous parameters have been calculated
The spot size is usually measured in air inside a treatment room during the commissioning procedure or a QA protocol. For instance, the following plot shows the measurements (blue stars) taken at 5 different positions around the isocenter for a 100 MeV beam in a cyclotron facility.
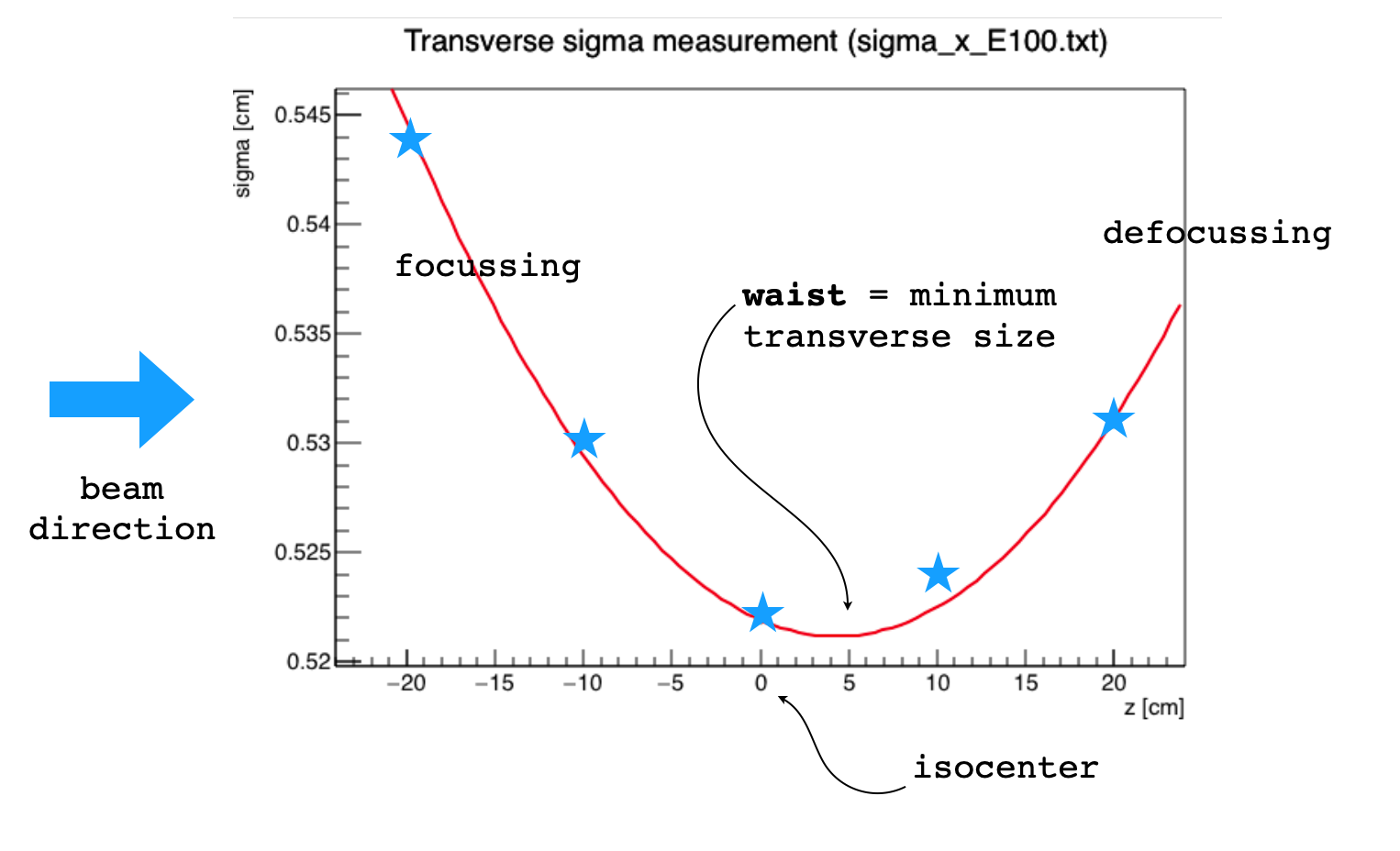
By fitting a parabolic function through the squares of the measured points
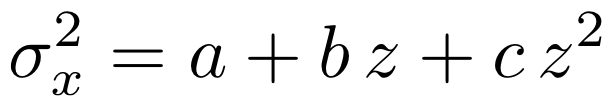
we can obtain the parameters needed for the emittance model

Example of a simple calculation in python using the measurements of previous Figure
from math import *
import numpy as np
zmeas = np.array([-20,-10,0,10,20])
sigmeas = np.array([0.544,0.530,0.522,0.524,0.531])
[[c,b,a],cov] = np.polyfit(zmeas,sigmeas*sigmeas,2,cov=True)
eps = sqrt(a*c-b*b/4)
alpha=-b/2/eps
beta=a/eps
print('epsilon=',eps)
print('alpha=',alpha)
print('beta=',beta)
which gives in output
epsilon= 0.0032824274429144556
alpha= 0.05220831320123199
beta= 83.25066186389999
Important
In the previous example, the parameters have been obtained with respect to the isocenter position which is at coordinate z=0 cm along the propagation direction. Since particles are generated in the field FoR, we have to inform FRED of the distance from field origin to the isocenter in order to have the correct spot size evolution along the beam axis. To this purpose, we have to use the emittanceRefPlaneDistance parameter.
Finally, the input lines for source definition are
field: 1 ; O = [0,0,-55]; L=[10,10,20]; pivot = [0.5,0.5,0.2]
pb<
ID = 1 ;
fieldID = 1
particle = proton
T = 100 # MeV
Xsec = emittance
twissAlphaX=0.05220831320123199
twissBetaX=83.25066186389999
emittanceX=0.0032824274429144556
emittanceRefPlaneDistance=55; # Field_1 origin is at 55 cm from ISO
pb>
The evolution of beam cross section using the emittance model is represented by the following Figure
